Cu toții suntem familiarizați cu situația când ne-am bazat pe intuiția noastră în loc de calcul sobru. La urma urmei, trebuie să recunoaștem că este departe de a fi întotdeauna posibil să calculăm totul înainte de a face o alegere. Și oricât de vicleni ar fi oamenii obișnuiți să facă alegerea numai după o analiză atentă, nu au trebuit să o facă odată conform principiului „probabil așa”. Unul dintre motivele unei astfel de acțiuni poate fi lipsa banală a timpului necesar pentru a evalua situația.
În același timp, o alegere așteaptă situația actuală chiar acum și nu permite evitarea unui răspuns sau acțiune. Dar situații și mai dificile pentru noi, care literalmente provoacă spasme cerebrale, sunt distrugerea încrederii în corectitudinea alegerii sau în probabila sa superioritate față de alte opțiuni bazate pe inferențe logice. Toate paradoxurile existente se bazează pe acest lucru.
Paradoxul jocului emisiunii TV „Let’s Make a Deal”
Unul dintre paradoxurile care stârnește dezbateri aprinse printre entuziaștii puzzle-ului se numește paradoxul Monty Hall. Acesta poartă numele gazdei unei emisiuni de televiziune din Statele Unite numită „Let’s Make a Deal”. La o emisiune TV, prezentatorul se oferă să deschidă una dintre cele trei uși, unde mașina este premiată, în timp ce în spatele celorlalte două este o capră.


După cum sugerează bunul simț, probabilitatea de a alege un lingou și de a câștiga în acest caz este de 1/2. Dar, în realitate, situația este diferită! "Dar cum este, totul este evident aici?" - tu intrebi. Să presupunem că ați ales numărul de celulă 1. Intuitiv, da, indiferent care a fost alegerea dvs. inițial, la final aveți efectiv înainte de a alege o monedă și un lingou. Și dacă inițial ați avut probabilitatea de a obține un premiu de 1/3, atunci la final, când un bancher deschide o celulă, veți obține o probabilitate de 1/2. Probabilitatea părea să crească de la 1/3 la 1/2. O analiză atentă a jocului arată că atunci când decizia este modificată, probabilitatea crește la 2/3 în loc de 1/2 intuitiv. Să vedem cum se întâmplă acest lucru.
Explicația creșterii probabilității
Spre deosebire de nivelul intuitiv, în care conștiința noastră consideră evenimentul de după schimbarea celulei ca ceva separat și uită de alegerea inițială, matematica nu rupe aceste două evenimente, ci, dimpotrivă, păstrează lanțul evenimentelor de la început până la sfârșit. Deci, așa cum am spus mai devreme, avem 1/3 șanse de a câștiga atunci când lovești un lingou, iar probabilitatea ca să alegem o celulă cu o monedă este de 2/3 (deoarece avem un lingou și două monede).
În continuare, vom descrie toate cazurile posibile ale dezvoltării evenimentelor sub condiția comportamentului clasic menționat anterior al liderului, în cazul nostru un bancher.
- Selectăm inițial o cutie de valori cu un lingou - probabilitate 1/3.
- Dacă jucătorul își schimbă alegerea acceptând oferta bancherului, el pierde.
- Dacă jucătorul nu schimbă alegerea fără să accepte oferta bancherului, el câștigă.
- Alegerea unei cutii de valori cu o monedă la prima încercare - probabilitate 2/3.
- Dacă jucătorul își schimbă alegerea, el a câștigat.
- Dacă jucătorul nu schimbă alegerea, pierde.
Pentru a înțelege acest paradox și a ieși din cătușele șablonului alegerii inițiale și a celulelor rămase, să ne imaginăm comportamentul jucătorului exact opusul. Înainte ca bancherul să propună o celulă pentru selecție, jucătorul este hotărât mental că își schimbă alegerea și numai după aceea urmează pentru el deschiderea unei uși suplimentare. De ce nu? La urma urmei, o ușă deschisă nu îi oferă mai multe informații într-o astfel de succesiune logică. În prima etapă a timpului, jucătorul împarte celulele în două zone diferite: prima este o zonă cu o celulă cu selecția sa originală, a doua cu două celule rămase. Apoi, jucătorul trebuie să facă o alegere între două zone. Probabilitatea de a obține o bară de aur din prima zonă este 1/3, din a doua 2/3. Selecția urmează o a doua zonă în care poate deschide două celule, prima va deschide bancherul, a doua el însuși.
Există o explicație și mai clară pentru paradoxul Monty Hall. Pentru aceasta este necesar să modificați formularea sarcinii. Bancherul arată clar că există o bară de aur într-una din cele trei celule ale băncii. În primul caz, el oferă să deschidă una din cele trei celule, iar în al doilea - două simultan. Ce va alege jucătorul? Ei bine, desigur, două deodată, datorită dublării probabilității. Și în momentul în care bancherul a deschis o celulă cu o monedă, acest lucru de fapt nu ajută jucătorul și nu îi împiedică alegerea, deoarece oricum bancherul va arăta această celulă cu o monedă, astfel încât jucătorul poate pur și simplu ignora această acțiune. Din partea jucătorului, nu poți decât să îi mulțumești bancherului pentru că i-a ușurat viața și, în loc de două, a trebuit să deschidă o celulă. Ei bine, și în cele din urmă, puteți scăpa de sindromul paradoxului dacă vă puneți în locul bancherului, care inițial știe că jucătorul din două din trei cazuri indică ușa greșită. Pentru bancher, nu există un paradox ca atare, deoarece într-o astfel de inversare a evenimentelor este sigur că în cazul unei schimbări de evenimente, jucătorul ia o bară de aur.

Paradoxul Monty Hall nu permite în mod clar să câștige conservatorii, care stau ferm în alegerea inițială și își pierd șansa de a crește probabilitatea. Pentru conservatori, va rămâne 1/3. Pentru oamenii vigilenți și judicioși, acesta crește până la 2/3 de mai sus.
Toate declarațiile de mai sus sunt relevante numai în conformitate cu condițiile convenite inițial.
Ce se întâmplă dacă creștem numărul de celule?
Ce se întâmplă dacă creștem numărul de celule? Să presupunem că, în loc de trei, vor fi 50. Lingoul de aur va sta doar într-o singură celulă, iar în restul de 49 - monede. În consecință, spre deosebire de cazul clasic, probabilitatea de a atinge ținta în mișcare este de 1/50 sau 2% în loc de 1/3, în timp ce probabilitatea de a alege o celulă cu o monedă este de 98%. Mai mult, situația se dezvoltă, ca în cazul anterior. Bancherul oferă să deschidă oricare dintre cele 50 de celule, pe care participantul le alege. Să presupunem că jucătorul deschide o celulă sub numerele de serie 49. Bankerul, la rândul său, ca și în versiunea clasică, nu se grăbește să îndeplinească dorința jucătorului și deschide alte 48 de celule cu monede și oferă să-și schimbe alegerea cu cea rămasă sub numărul 50.
Este important să înțelegem aici că bancherul deschide exact 48 de celule și nu 30 și pleacă în același timp cu 2, inclusiv pe cea aleasă de jucător. Această alegere permite paradoxului să contravină intuiției. Ca și în cazul variantei clasice, deschiderea de 48 de celule a bancherului lasă o singură alternativă din care să aleagă. Cazul unei variante cu o deschidere mai mică de celule nu ne permite să punem problema la egalitate cu cea clasică și să simțim paradoxul.
Dar, din moment ce am atins această opțiune, să presupunem că bancherul nu lasă una, cu excepția celei alese de jucător, ci mai multe celule. A prezentat, ca și până acum, 50 de celule. După alegerea unui jucător, bancherul deschide o singură celulă, lăsând 48 de celule închise, inclusiv cea selectată de jucător. Probabilitatea de a alege un lingou prima dată este 1/50. În total, probabilitatea de a găsi un lingou în celulele rămase este de 49/50, care, la rândul său, este răspândită nu la 49, ci la 48 de celule. Nu este dificil de calculat că probabilitatea de a găsi un lingou în această variantă este (49/50) / 48 = 49/2900. Probabilitatea, deși nu multă, dar totuși mai mare de 1/50 cu aproximativ 1%.
Diagrama comportamentului Monty Hall
După cum am menționat la început, Monty Hall, lider în scenariul clasic al unui joc cu uși, capre și o mașină premiată, poate schimba condițiile jocului și, împreună cu acesta, probabilitatea de a câștiga.
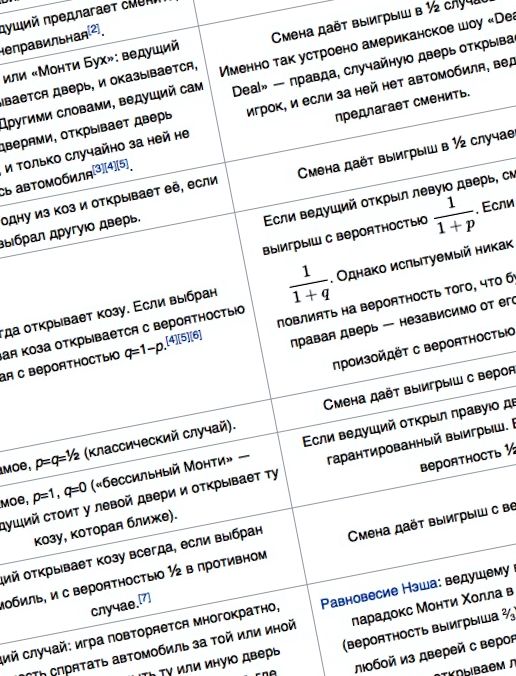
Diagrama comportamentului Monty Hall.
Paradox matematică
Pot formula matematice să dovedească o creștere a probabilității atunci când se schimbă o alegere?
Să reprezentăm lanțul evenimentelor ca un set împărțit în două părți, prima parte va fi luată ca X - aceasta este alegerea jucătorului pentru celula sigură din prima etapă; iar al doilea set Y este celelalte două celule rămase. Probabilitatea (B) de a câștiga pentru celulele 2 și 3 poate fi exprimată folosind formulele.
B (2) = 1/2 * 2/3 = 1/3
B (3) = 1/2 * 2/3 = 1/3
Unde 1/2 este probabilitatea cu care bancherul va deschide celulele 2 și 3, cu condiția ca jucătorul să aleagă inițial o celulă fără un lingou.
Mai mult, probabilitatea condițională 1/2 când un bancher deschide o celulă cu o monedă se schimbă cu 1 și 0. Apoi formulele iau următoarea formă:
B (2) = 0 * 2/3 = 0
B (3) = 1 * 2/3 = 1
Aici vedem clar că probabilitatea de a alege un lingou în celula 3 este de 2/3, care este puțin peste 60 la sută.
Un programator foarte entry-level poate verifica cu ușurință acest paradox scriind un program care calculează probabilitatea atunci când alege o alegere sau invers și verifică rezultatele.
Paradoxul explicat în filmul 21 (Douăzeci și unu)
O explicație clară a paradoxului lui Monty Paul este dată în filmul „21” (Douăzeci și unu), în regia lui Robert Luketic. La prelegere, profesorul Mickey Rosa dă un exemplu din spectacolul Let’s Make a Deal și pune o întrebare despre distribuția probabilității elevului Ben Campbell (actor și cântăreț James Anthony), care oferă alinierea corectă și, prin urmare, îl surprinde pe profesor.
Auto-studiu al paradoxului
Pentru persoanele care doresc să verifice singur rezultatul în practică, dar care nu au o bază matematică, vă propunem să simulați independent un joc în care veți fi lider, iar cineva va fi jucătorul. Puteți implica copiii în acest joc, care vor alege bomboane sau ambalaje de bomboane din ele în cutii de carton pre-pregătite. Cu fiecare alegere, asigurați-vă că înregistrați rezultatul pentru calcul ulterior.