Cel mai mare divizor comun al numerelor (GCD) cum se găsește și aplicarea sa în practică

Astăzi răspundem la întrebarea „Care este cel mai mare număr comun de divizare (prescurtat ca GCD)? " din cursul matematicii fundamentale. Astăzi acest subiect este considerat ca parte a studiului unui program de matematică în clasa a 5-a.

Numele în sine arată clar că GCD de numere este cel mai mare număr prin care o serie de numere poate fi împărțită fără rest. Toate numerele din seria prezentată ar trebui să împărtășească acest total. În cadrul școlii, un număr de numere sunt prezentate sub forma a două numere pentru ușurarea asimilării materialului. În materialul nostru, vom explica nu numai cum să găsim cel mai mare divizor comun al numerelor, ci și aplicarea practică a acestei reguli folosind un exemplu din viața reală. Deci să mergem.

Cum se găsește cel mai mare divizor comun al numerelor?

Să începem cu un exemplu simplu în cadrul numerelor din două cifre prezentate în tabelul de înmulțire. De exemplu, avem trei numere 72, 60 și 18 pentru care este necesar să găsim GCD. Începem să listăm divizorul de la cel mai mic la cel mai mare. O serie din aceste trei numere sunt divizibile cu 2, 3, 6. Deci GCD (72, 60, 18) = 6. Aceasta este așa-numita metodă de selecție.

Notă importantă. Toate numerele de pe rând vor avea întotdeauna un GCD. Nu poate lipsi deloc într-o serie de numere întregi. Numerele care nu au mai mulți divizori comuni vor fi întotdeauna divizibile cu 1. De exemplu, pentru numere precum 6,7,8, GCD va fi 1.

În plus față de selecție, există o metodă mai metodică, care vă permite să găsiți GCD prin contorizarea fiecărui număr în factori.

1. Pentru fiecare număr prezentat, găsim cel mai mic divizor mai mare decât unul.
2. Mai mult, pentru fiecare număr obținut în timpul divizării, la rândul nostru găsim cel mai mic divizor al nostru, conform unei scheme similare. În rezultatul final, atunci când împărțim ultimul număr, obținem unul.
3. Găsim factorii comuni care apar la extinderea seriei noastre.
4. Înmulțindu-le, obținem GCD.

Pe o tablă albă, am extins fiecare număr din seria noastră și am obținut divizorii totali, care se repetă în fiecare rând. Acestea sunt numerele 2 și 3. Astfel, înmulțindu-le obținem 6. GCD (72,60, 18) = 6.

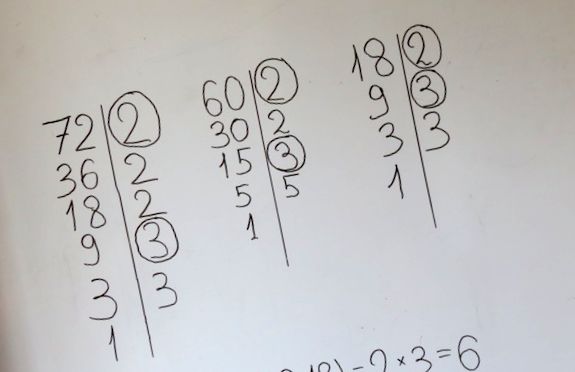
Ei bine, în concluzie, vom încerca să găsim un exemplu din viața noastră, unde ar putea fi necesare cunoștințe despre calcularea GCD.

Videoclip în care un profesor de matematică arată cum să găsească GCD.

Sarcină practică folosind GCD

Vara, studenții satului Perekop, din cauza condițiilor de mediu deteriorate, trebuie să meargă la tabăra „Artek”. S-a decis separarea tuturor băieților și fetelor în diferite autobuze. Numărul de fete din școală este de 60, băieți - 72. Este necesar să alegeți o flotă de autobuze cu atâtea locuri, astfel încât toate locurile să fie ocupate fără rest. Și calculați, de asemenea, numărul necesar de astfel de autobuze.

Decizie. Pentru a determina tipul de autobuz cu numărul de locuri, cu condiția ca băieții și fetele să fie cazați în autobuze separate fără locuri în exces, este necesar să se utilizeze calculul GCD (60, 72). Divizorul comun maxim este 12. Astfel, aveți nevoie de un autobuz cu numărul de locuri permise - 12. Cunoscând numărul de locuri din fiecare autobuz, puteți calcula numărul necesar de autobuze pentru băieți și fete și numărul total al acestora. Pentru transportul băieților, sunt necesare 72: 12 = 6 autobuze. Pentru fete 60: 12 = 5 autobuze. Numărul total de autobuze 11.

Ne vom bucura dacă vă oferiți variantele de sarcini practice folosind cel mai mare divizor comun al numerelor pentru a distruge un tipar neplăcut creat în raport cu matematica, și anume, în absența unei aplicații de viață a materialului studiat la un curs școlar de matematică. Exemplul prezentat mai sus sugerează că acest lucru este departe de a fi cazul.