Înainte de a studia fracțiuni în programa școlară de clasa a 5-a la matematică, ei studiază subiectul celui mai mic multiplu comun sau abreviat ca LCM. În cadrul articolelor noastre, oferim nu numai o definiție și reguli pentru găsirea unor astfel de lucruri, ci și prezentăm în mod necesar exemple practice unde pot fi aplicate.
Deci, să începem cu un concept. Ce este un NOC? Cel mai mic multiplu comun de numere X și Y sunt egale cu cel mai mic număr întreg prin care aceiași X și Y sunt divizibili uniform.

Găsiți cel mai mic multiplu comun de numere înainte de a adăuga sau scădea fracțiile
Materialul pentru calcularea NOC în cursul curriculumului școlar din clasa a V-a nu este dat doar înainte de studiul fracțiilor. Faptul este că astfel de operații cu fracții precum adunarea sau scăderea trebuie aduse într-un numitor comun pentru fiecare număr fracțional.
Pentru ușurarea asimilării materialului, vom începe să determinăm LCM pentru o pereche de numere naturale întregi în tabelul de înmulțire. De exemplu, există două numere 6 și 16. Dacă utilizați metoda de selecție, puteți găsi cu ușurință cel mai mic număr care împarte 6 și 16. Acest număr va fi egal cu 48. Cu toate acestea, această metodă de selecție se aplică doar numerelor prime. Dar dacă trebuie să găsiți LCM pentru numere în afara tabelului de înmulțire. Se pare că în astfel de cazuri există o tehnică de găsire.
Regula pentru găsirea NOC
Regula pentru a găsi cel mai mic multiplu comun dintr-o serie de numere poate fi reprezentată ca următorul algoritm:
- Descompunem fiecare număr în factori primi.
- Apoi, din fiecare rând de numere descompuse, scriem numere care au valori comune.
- Dintre acele numere care sunt prezente în fiecare serie extinsă, le scriem doar pe cele care au cel mai mare grad.
- Înmulțim numerele în puterile corespunzătoare.
Ca exemplu de calcul al LCM conform acestei reguli, luăm două numere 14 și 16.
16 = 2 x 2 x 4 = 22 x 4
20 = 2 x 2 x 5 = 22 x 5
LCM = 22 x 4 x 5 = 80
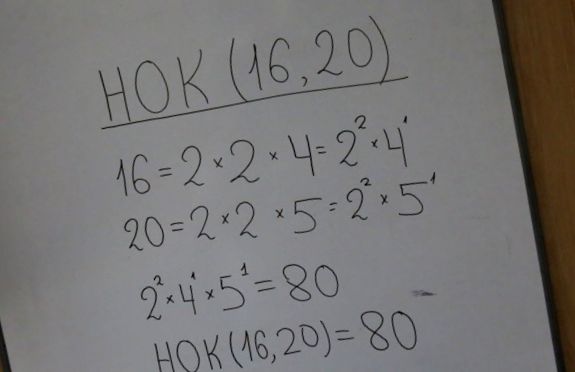
Ei bine, în mod tradițional, să trecem la aplicația practică de a găsi NOC.
Problema utilizării LCM
Din autogara din Sevastopol, două autobuze pleacă simultan pe rute diferite. Primul autobuz Mercedes va călători către Krasnodar și înapoi în 16 ore, iar al doilea autobuz Ikarus către Anapa și înapoi va parcurge ruta în 20 de ore. Ora pentru opriri la punctele de plecare și de sosire este aceeași și este deja inclusă în condițiile 16 și 20 de ore condiționate. Condiții pentru urmărirea lor continuă.
Decizie. Plecând din Sevastopol, două autobuze urmează rute diferite și se întorc la punctul de plecare la ore diferite. Când autobuzul Ikarus se întoarce din Anapa, autobuzul Mercedes va părăsi Sevastopolul pentru a doua oară și va fi din nou pe drum. Aceste autobuze se vor întâlni din nou la Sevastopol la anumite intervale de timp. Și pentru a afla după ce oră se vor întâlni, trebuie să găsiți cel mai mic multiplu comun. Folosind regula pentru calcularea LCM, prezentată mai sus, obținem timpul întâlnirii lor în 80 de ore.
Aici suntem din nou convinși că o astfel de regulă are dreptul să fie aplicată în practică în viață. Dacă aveți propriile sarcini practice pentru găsirea NOC, atunci le puteți lăsa în comentarii și cu siguranță le vom include în publicație.